Comparison between original KR algorithm and gcMapExplorer implementation¶
Here, we compare the results from original KR matrix balancing algorithm with the gcMapExplorer implmentation.
Note: Since orignal argorithm is implemented in MATLAB, here we used Octave for calculation. Also, oct2py python module should be installed on the system.
Note
- Below we use already normalized maps that were calculated during previous tutorial.
Importing required modules:
- gcMapExplorer.lib
- numpy for statistics
- matplotlib for plotting
- oct2py acts as bridge between Python and Octave, to run original algorithm
[1]:
import gcMapExplorer.lib as gmlib
import numpy as np
from oct2py import octave
import matplotlib as mpl
import matplotlib.pyplot as plt
# To show inline plots
%matplotlib inline
plt.style.use('ggplot') # Theme for plotting
Here we write original code in norm_KR.m file in current directory, which will be used below for calculation.
[2]:
def write_orig_matlab_code():
code = """function [x,res] = norm_KR(A,tol,x0,delta,Delta,fl)
% BNEWT A balancing algorithm for symmetric matrices
%
% X = norm_KR(A) attempts to find a vector X such that
% diag(X)*A*diag(X) is close to doubly stochastic. A must
% be symmetric and nonnegative.
%
% X0: initial guess. TOL: error tolerance.
% delta/Delta: how close/far balancing vectors can get
% to/from the edge of the positive cone.
% We use a relative measure on the size of elements.
% FL: intermediate convergence statistics on/off.
% RES: residual error, measured by norm(diag(x)*A*x - e).
% Initialise
n = size(A,1); e = ones(n,1); res=[];
if nargin < 6, fl = 0; end
if nargin < 5, Delta = 3; end
if nargin < 4, delta = 0.1; end
if nargin < 3, x0 = e; end
if nargin < 2, tol = 1e-4; end
% Inner stopping criterion parameters.
g=0.9; etamax = 0.1;
eta = etamax; stop_tol = tol*.5;
x = x0; rt = tol^2; v = x.*(A*x); rk = 1 - v;
rho_km1 = rk'*rk; rout = rho_km1; rold = rout;
MVP = 0; % We'll count matrix vector products.
i = 0; % Outer iteration count.
if fl == 1, fprintf('it in. it res'), end
while rout > rt % Outer iteration
i = i + 1; k = 0; y = e;
innertol = max([eta^2*rout,rt]);
while rho_km1 > innertol %Inner iteration by CG
k = k + 1;
if k == 1
Z = rk./v; p=Z; rho_km1 = rk'*Z;
else
beta=rho_km1/rho_km2;
p=Z + beta*p;
end
% Update search direction efficiently.
w = x.*(A*(x.*p)) + v.*p;
alpha = rho_km1/(p'*w);
ap = alpha*p;
% Test distance to boundary of cone.
ynew = y + ap;
if min(ynew) <= delta
if delta == 0
break
end
ind = find(ap < 0);
gamma = min((delta - y(ind))./ap(ind));
y = y + gamma*ap;
break
end
if max(ynew) >= Delta
ind = find(ynew > Delta);
gamma = min((Delta-y(ind))./ap(ind));
y = y + gamma*ap;
break
end
y = ynew;
rk = rk - alpha*w; rho_km2 = rho_km1;
Z = rk./v; rho_km1 = rk'*Z;
end
x = x.*y; v = x.*(A*x);
rk = 1 - v; rho_km1 = rk'*rk; rout = rho_km1;
MVP = MVP + k + 1;
% Update inner iteration stopping criterion.
rat = rout/rold; rold = rout; res_norm = sqrt(rout);
eta_o = eta; eta = g*rat;
if g*eta_o^2 > 0.1
eta = max([eta,g*eta_o^2]);
end
eta = max([min([eta,etamax]),stop_tol/res_norm]);
if fl == 1
fprintf('%3d %6d %.3e', i,k, r_norm);
res=[res; r_norm];
end
end
fprintf('Matrix-vector products = %6d', MVP)
"""
fout = open('norm_KR.m', 'w')
fout.write(code)
fout.close()
Wrapper function to normalize map using original algorithm
Follwing function perform several steps:
- Extract a new matrix from input matrix by removing any rows and columns with missing data
- Normalize it using Octave
- Construct normalized matrix from normalization vector
- Expand normalized matrix by re-inserting rows and column with missing data
[3]:
def get_norm_KR_matlab(ccmap):
# Discard rows and columns with missing data
ccmap.make_readable()
bNonZeros = gmlib.ccmapHelpers.get_nonzeros_index(ccmap.matrix)
A = (ccmap.matrix[bNonZeros,:])[:,bNonZeros]
# Calculate normalization vector using original MATLAB code
vector = octave.norm_KR(A[:])
# Construct KR normalized matrix using normalization vector
outA = vector.T * (A * vector)
# Initialize ouput ccmap object
normCCMap = ccmap.copy(fill=0.0)
normCCMap.make_editable()
normCCMap.bNoData = ~bNonZeros
# Store normalized values to output ccmap
dsm_i = 0
ox = normCCMap.matrix.shape[0]
idx_fill = np.nonzero( ~normCCMap.bNoData )
for i in range(ox):
if not normCCMap.bNoData[i]:
normCCMap.matrix[i, idx_fill] = outA[dsm_i]
normCCMap.matrix[idx_fill, i] = outA[dsm_i]
dsm_i += 1
# Get the maximum and minimum value except zero
ma = np.ma.masked_equal(outA, 0.0, copy=False)
normCCMap.minvalue = ma.min()
normCCMap.maxvalue = ma.max()
normCCMap.make_unreadable()
ccmap.make_unreadable()
return normCCMap
Normalization using original Matlab code¶
Here, we read raw maps from a gcmap file, normalize it using above function and save the normalized maps to output gcmap file.
[4]:
gcMapInputFile = 'cmaps/CooMatrix/rawObserved_100kb.gcmap'
gcMapOutFile = 'norm_comparison/normKR_matlab.gcmap'
write_orig_matlab_code()
# Get list of maps in ascending order
gcmap = gmlib.gcmap.GCMAP(gcMapInputFile)
gcmap.loadSmallestMap()
mapList = gcmap.mapNameList.copy()
del gcmap
for mapName in mapList:
print('Calculating for {0}...'.format(mapName))
ccMap = gmlib.gcmap.loadGCMapAsCCMap(gcMapInputFile, mapName=mapName)
normKR_ccmap = get_norm_KR_matlab(ccMap)
if normKR_ccmap is not None:
gmlib.gcmap.addCCMap2GCMap(normKR_ccmap, gcMapOutFile,generateCoarse=True, coarsingMethod='sum',)
del ccMap
del normKR_ccmap
Calculating for chr21...
Matrix-vector products = 36
INFO:addCCMap2GCMap: Opened file [norm_comparison/normKR_matlab.gcmap] for reading writing..
INFO:addCCMap2GCMap: Data for chr21 is already present in [norm_comparison/normKR_matlab.gcmap], replacing it...
INFO:addCCMap2GCMap: Adding data to [norm_comparison/normKR_matlab.gcmap] for [chr21] ...
INFO:addCCMap2GCMap: ...Finished adding data for [chr21] ...
INFO:addCCMap2GCMap: Generating downsampled maps for [chr21] ...
INFO:addCCMap2GCMap: ... Finished downsampling for [chr21] ...
INFO:addCCMap2GCMap: Closed file [norm_comparison/normKR_matlab.gcmap]...
Calculating for chr22...
Matrix-vector products = 31
INFO:addCCMap2GCMap: Opened file [norm_comparison/normKR_matlab.gcmap] for reading writing..
INFO:addCCMap2GCMap: Data for chr22 is already present in [norm_comparison/normKR_matlab.gcmap], replacing it...
INFO:addCCMap2GCMap: Adding data to [norm_comparison/normKR_matlab.gcmap] for [chr22] ...
INFO:addCCMap2GCMap: ...Finished adding data for [chr22] ...
INFO:addCCMap2GCMap: Generating downsampled maps for [chr22] ...
INFO:addCCMap2GCMap: ... Finished downsampling for [chr22] ...
INFO:addCCMap2GCMap: Closed file [norm_comparison/normKR_matlab.gcmap]...
Calculating for chr20...
Matrix-vector products = 29
INFO:addCCMap2GCMap: Opened file [norm_comparison/normKR_matlab.gcmap] for reading writing..
INFO:addCCMap2GCMap: Data for chr20 is already present in [norm_comparison/normKR_matlab.gcmap], replacing it...
INFO:addCCMap2GCMap: Adding data to [norm_comparison/normKR_matlab.gcmap] for [chr20] ...
INFO:addCCMap2GCMap: ...Finished adding data for [chr20] ...
INFO:addCCMap2GCMap: Generating downsampled maps for [chr20] ...
INFO:addCCMap2GCMap: ... Finished downsampling for [chr20] ...
INFO:addCCMap2GCMap: Closed file [norm_comparison/normKR_matlab.gcmap]...
Calculating for chr15...
Matrix-vector products = 37
INFO:addCCMap2GCMap: Opened file [norm_comparison/normKR_matlab.gcmap] for reading writing..
INFO:addCCMap2GCMap: Data for chr15 is already present in [norm_comparison/normKR_matlab.gcmap], replacing it...
INFO:addCCMap2GCMap: Adding data to [norm_comparison/normKR_matlab.gcmap] for [chr15] ...
INFO:addCCMap2GCMap: ...Finished adding data for [chr15] ...
INFO:addCCMap2GCMap: Generating downsampled maps for [chr15] ...
INFO:addCCMap2GCMap: ... Finished downsampling for [chr15] ...
INFO:addCCMap2GCMap: Closed file [norm_comparison/normKR_matlab.gcmap]...
Calculating for chr5...
Matrix-vector products = 102
INFO:addCCMap2GCMap: Opened file [norm_comparison/normKR_matlab.gcmap] for reading writing..
INFO:addCCMap2GCMap: Data for chr5 is already present in [norm_comparison/normKR_matlab.gcmap], replacing it...
INFO:addCCMap2GCMap: Adding data to [norm_comparison/normKR_matlab.gcmap] for [chr5] ...
INFO:addCCMap2GCMap: ...Finished adding data for [chr5] ...
INFO:addCCMap2GCMap: Generating downsampled maps for [chr5] ...
INFO:addCCMap2GCMap: ... Finished downsampling for [chr5] ...
INFO:addCCMap2GCMap: Closed file [norm_comparison/normKR_matlab.gcmap]...
Calculating for chr1...
Matrix-vector products = 105
INFO:addCCMap2GCMap: Opened file [norm_comparison/normKR_matlab.gcmap] for reading writing..
INFO:addCCMap2GCMap: Data for chr1 is already present in [norm_comparison/normKR_matlab.gcmap], replacing it...
INFO:addCCMap2GCMap: Adding data to [norm_comparison/normKR_matlab.gcmap] for [chr1] ...
INFO:addCCMap2GCMap: ...Finished adding data for [chr1] ...
INFO:addCCMap2GCMap: Generating downsampled maps for [chr1] ...
INFO:addCCMap2GCMap: ... Finished downsampling for [chr1] ...
INFO:addCCMap2GCMap: Closed file [norm_comparison/normKR_matlab.gcmap]...
Correlation Calculation¶
Below we calculate correlation between above normalized maps (original algorithm) and previously normalized maps (gcMapExplorer implementation).
[5]:
gcMapOne = 'norm_comparison/normKR_matlab.gcmap'
gcMapTwo = 'normalized/normKR_100kb.gcmap'
mapList, corrs, pvalues = gmlib.cmstats.correlateGCMaps(gcMapOne, gcMapTwo, corrType='pearson')
print('Pearson Correlation gcMapExplorer-KR vs original-KR')
print('====================================================')
print('\nChromosome Corr P-values')
print('--------------------------------------------------------')
for i in range(len(mapList)):
print('{0:5} {1:12.5} {2:12.5}'.format( mapList[i], corrs[i], pvalues[i]))
print('--------------------------------------------------------')
INFO:correlateGCMaps: Performing calculation for chr1 ...
INFO:correlateGCMaps: Finished calculation for chr1 ...
INFO:correlateGCMaps: Performing calculation for chr5 ...
INFO:correlateGCMaps: Finished calculation for chr5 ...
INFO:correlateGCMaps: Performing calculation for chr15 ...
INFO:correlateGCMaps: Finished calculation for chr15 ...
INFO:correlateGCMaps: Performing calculation for chr20 ...
INFO:correlateGCMaps: Finished calculation for chr20 ...
INFO:correlateGCMaps: Performing calculation for chr21 ...
INFO:correlateGCMaps: Finished calculation for chr21 ...
INFO:correlateGCMaps: Performing calculation for chr22 ...
INFO:correlateGCMaps: Finished calculation for chr22 ...
Pearson Correlation gcMapExplorer-KR vs original-KR
====================================================
Chromosome Corr P-values
--------------------------------------------------------
chr1 1.0 0.0
chr5 1.0 0.0
chr15 1.0 0.0
chr20 1.0 0.0
chr21 1.0 0.0
chr22 1.0 0.0
--------------------------------------------------------
Results¶
As can be seen above output table, both normalized maps correlate perfectly, therefore, gcMapExplorer implemented normalization yielded almost same result as of the original algorithm.
To plot comparison between values from original and gcMapExplorer method
Below function is used to plot values from a single map.
[6]:
def plot_comparison_for_chromosome(mapName, fig, idx):
# Read normalized map from original algorithm
matlabNormCCmap = gmlib.gcmap.loadGCMapAsCCMap('norm_comparison/normKR_matlab.gcmap', mapName=mapName)
# Read normalized map from gcMapExplorer implemented code
gcMapExpNormCCmap = gmlib.gcmap.loadGCMapAsCCMap('normalized/normKR_100kb.gcmap', mapName=mapName)
# Make ccmap matrix file available for reading
matlabNormCCmap.make_readable()
gcMapExpNormCCmap.make_readable()
# Mask any bins that have zero value, since both map are calculated from same raw map,
# same bins will have missing data
matlabNormCCmapMasked = np.ma.masked_equal(matlabNormCCmap.matrix, 0.0, copy=False)
gcMapExpNormCCmapMasked = np.ma.masked_equal(gcMapExpNormCCmap.matrix, 0.0, copy=False)
ax = fig.add_subplot(3,2,idx) # Axes plot
ax.set_yscale("log", basey=10, nonposy='clip') # Set Y-axis to log scale
ax.set_xscale("log", basey=10, nonposy='clip') # Set X-axis to log scale
ax.set_title('Comparison {0}'.format(mapName)) # Title plot
# Plot for Pearson correlation
# Plot only those bins that do not have missing data (> zero)
ax.scatter(matlabNormCCmapMasked.compressed(), gcMapExpNormCCmapMasked.compressed(), marker='o', s=6)
ax.set_xlabel('Original KR Normalized values')
ax.set_ylabel('gcMapExplorer KR Normalized values')
del matlabNormCCmap
del gcMapExpNormCCmap
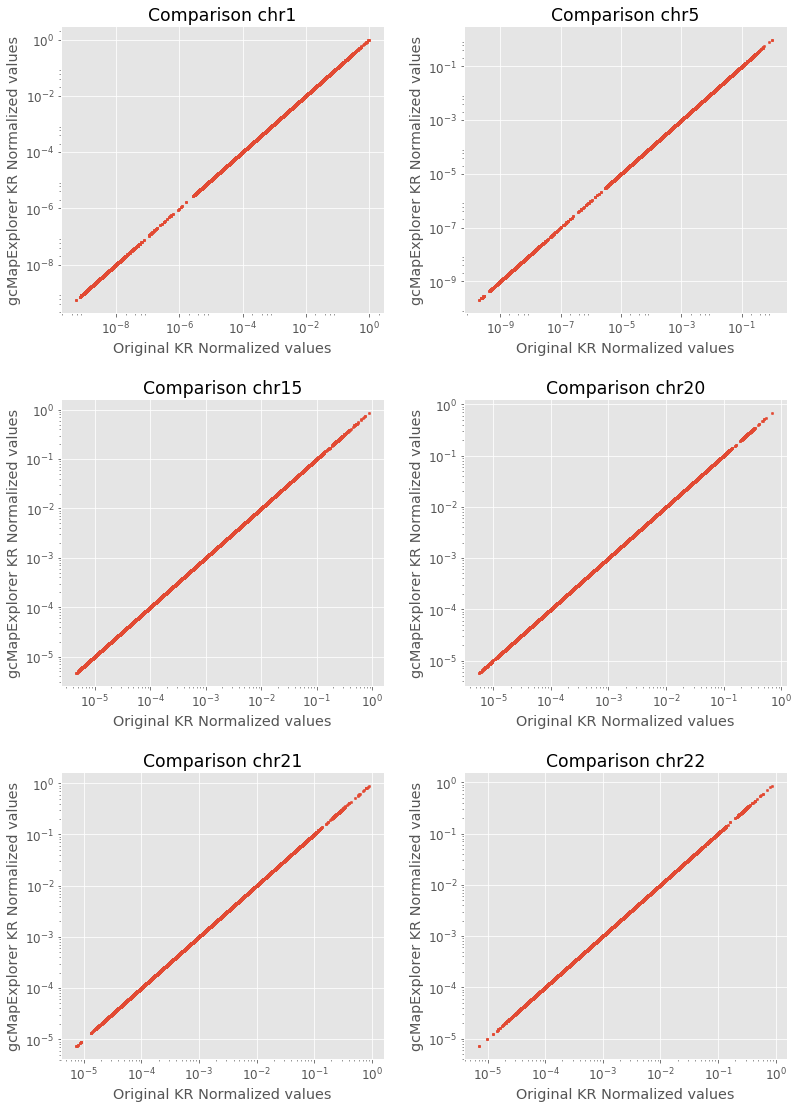
Now, we plot normalized values for some chromosome maps using above written function, which also shows that the obtaind values are similar from both implementations.
[7]:
fig = plt.figure(figsize=(13,19)) # Figure size
fig.subplots_adjust(hspace=0.3, wspace=0.25) # Space between sub-plots
mpl.rcParams.update({'font.size': 12}) # Font-size
# Plot for chromosomes
plot_comparison_for_chromosome('chr1', fig, 1) # For chr1
plot_comparison_for_chromosome('chr5', fig, 2) # For chr5
plot_comparison_for_chromosome('chr15', fig, 3) # For chr15
plot_comparison_for_chromosome('chr20', fig, 4) # For chr20
plot_comparison_for_chromosome('chr21', fig, 5) # For chr21
plot_comparison_for_chromosome('chr22', fig, 6) # For chr22
plt.savefig('compare_KR.png', dpi=300)
plt.show()